
Deret geometri dan deret aritmetika adalah suatu hal yang berbeda. Tapi tidak jarang juga, banyak orang belum bisa membedakan apa perbedaan di antara keduanya.
Nah, tulisan ini selain akan membedah tentang perbedaan antara deret geometri dan deret aritmatika, saya juga akan menjelaskan tentang pengertian, rumus deret geometri, contoh soal deret geometri, dan kuis deret geometri yang bisa kamu kerjakan dan langsung kamu ketahui berapa skor perolehanmu.
Yuk kita bahas satu persatu.
1# Apa itu Deret Geometri?
Pemahaman tentang deret geometri tidak akan sempurna jika kamu tidak memahami apa itu barisan geometri.
Barisan Geometri adalah barisan yang mempunyai perbandingan/rasio suku yang berdekatan selalu sama. Rasio dilambangkan dengan “r“.
Contoh Barisan Geometri :
2, 4, 8, 16, 32, 64, ….
Dari barisan tersebut, dapat diketahui rasionya dari suku-suku yang berdekatannya yaitu:
r = $latex \frac{U2}{U1} $
r = $latex \frac{4}{2} $
r = 2
Nah, jika kita telah mengetahui bahwa barisan bilangan tersebut merupakan barisan geometri, maka kita bisa menentukan deret geometrinya.
Deret Geometri adalah jumlah suku-suku pada barisan geometri.
Jadi, deret geometri dari 6 barisan geometri ini:
2, 4, 8, 16, 32, 64
adalah 2 + 4 + 8 + 16 + 32 + 64 = 126.
Apakah kamu sudah bisa memahami maksud dari deret geometri?
Jika sudah, kita lanjut ke materi yang lebih mendalam ya…
2# Apa perbedaannya antara deret geometri dan deret aritmatika?
Untuk membedakannya, kamu harus paham tentang apa itu barisan geometri dan apa itu barisan aritmatika ya..
Kita bahas :
ini contoh barisan geometri : 2, 4, 8, 16, 32, 64, …
ini contoh barisan aritmatika : 2, 4, 6, 8, 10, 12, 14, 16, …
Sudahkah kamu bisa membedakan di mana letak pembedanya?
Yupz, bedanya jika barisan geometri kita mengenal istilah rasio maka dalam barisan aritmatika kita mengenal istilah beda.
Rasio (disimbolkan dengan “r”) adalah perbandingan antara dua suku yang berdekatan pada barisan geometri. Sedangkan Beda (disimbolkan dengan “b”) adalah selisih antara dua suku yang berdekatan pada barisan aritmatika.
Nah, setelah kamu memahami barisan aritmatika dan barisan geometri, tentunya kamu sudah bisa membedakan apa itu deret aritmatika dan deret geometri.
Ya, benar.
Deret aritmatika merupakan jumlah n suku pertama pada barisan aritmatika.
Sedangkan deret geometri adalah jumlah n suku pertama pada barisan geometri.
Penjelasan lengkap mengenai deret aritmatika dapat kamu pelajari secara rinci pada link berikut ini:
Link : https://ciptacendekia.com/deret-aritmatika/
3# Rumus Deret Geometri
Untuk mempelajari rumus-rumus deret geometri, alangkah baiknya jika kita bahas dari contoh barisan geometri ya…
Misal ada barisan geometri seperti ini:
2, 4, 8, 16, 32, 64, …
maka suku pertama (ditulis a) atau disebut dengan U1 adalah 2.
Rumus mencari rasio
sekarang perhatikan antara suku ke-2 dan suku ke-1 nya.
rasio diperoleh dari perbandingan antara:
r = $latex \frac{4}{2} $
r = 2
atau dengan kata lain, rasio dapat dirumuskan sebagai berikut :
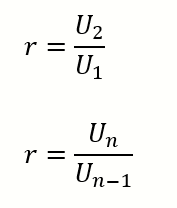
Setelah kamu mengetahui a dan r nya, sekarang kita akan pelajari rumus mencari suku ke-n ( Un) dan jumlah suku ke-n (Sn) dari suatu deret geometri.
Mencari Rumus Suku Ke-n
Perhatikan kembali pola barisan geometri berikut:
2, 4, 8, 16, 32, 64, …
r = 2
Suku ke-1 = 2 = a
Suku ke-2 = 4 = = 2 . 2 = 2. 21 = a r1
Suku ke-3 = 8 = 2. 4 = 2. 22 = a. r2
Suku ke-4 = 16 = 2. 8 = 2. 23 = a. r3
Suku ke-5 = 32 = 2. 16 = 2. 24 = a. r4
Suku ke-6 = 64 = 2. 32 = 2. 25 = a. r5
Suku ke-n = a. rn-1
Sehingga rumus suku ke-n dapat dirumuskan menjadi
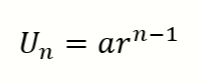
Keterangan:
- Un= suku ke-n yang hendak dicari
- a = suku pertama (awal)
- r = rasio
- n = urutan ke
Nah, untuk mengingat rumus tersebut, coba perhatikan kembali pola barisan geometrinya ya…
Sekarang, kita lanjut mencari deret geometrinya. Yaitu berapa jumlah suku ke-n nya.
Deret geometri atau deret ukur disimbolkan dengan Sn
Mencari Rumus Jumlah Suku Ke-n (Rumus Deret Geometri)
Perhatikan kembali pola barisan geometri ini ya sebagai contoh
2, 4, 8, 16, 32, 64, …
Sn = U1 + U2 + U3 + U4 + U5 + U6 + … + Un
Sn = a + ar1 + ar2 + ar3 + ar4 + ar5 + … + arn-1
Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita akan mendapatkan persamaan
dan jika kita rapihkan susunannya menjadi

Rumus ini biasa digunakan bila nilai rasio (r) < 1.
Sedangkan jika nilai rasionya > 1 maka menggunakan rumus berikut ini:

Di mana nilai r tidak boleh sama dengan 1.
Oke, di materi selanjutnya, kita akan belajar deret geometri tak hingga
4# Barisan dan Deret Geometri Tak Hingga
Barisan dan deret geometri tak hingga dibagi menjadi dua jenis, yaitu tak hingga divergen dan tak hingga konvergen.
Keduanya memiliki perbedaan yang cukup penting. Mari kita lihat pengertian dari kedua jenis barisan tak hingga tersebut beserta perbedaannya.
Deret Geometri Tak Hingga Divergen
Deret geometri tak hingga divergen adalah suatu deret yang nilai bilangannya semakin membesar dan tidak bisa dihitung jumlahnya. Bisa kita lihat seperti di bawah ini,
2, 4, 8, 16, 32, …
Jika ditanya berapa sih jumlah seluruhnya?
Jumlah seluruhnya tidak bisa dihitung karena nilainya semakin besar.
Deret Geometri Tak Hingga Konvergen
Berbeda dengan divergen, deret geometri tak hingga konvergen merupakan suatu deret di mana nilai bilangannya semakin mengecil dan dapat dihitung jumlahnya. Seperti di bawah ini,
8, 4, 2, 1, 1⁄2, 1⁄4, …
Semakin lama nilainya semakin mengecil dan ujungnya akan mendekati angka 0. Hal ini membuat deret geometri tak hingga konvergen dapat dihitung jika ditanyakan jumlah seluruhnya.
Lalu bagaimana caranya menghitung jumlah seluruh dari tak hingga konvergen?
Sebelum masuk ke rumus, ada syarat terlebih dahulu jika kamu bertemu dengan deret geometri tak hingga konvergen, yaitu rasionya atau pengalinya harus antara -1 sampai 1 (-1 > r > 1) dan ini berlaku untuk negatif maupun positif.
Nah sekarang kita lihat ya rumus menghitung jumlah tak hingga dari deret geometri berikut
8, 4, 2, 1, 1⁄2, 1⁄4, …
diketahui a = 8
r = 1⁄2
Maka deret tak hingganya adalah
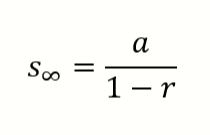
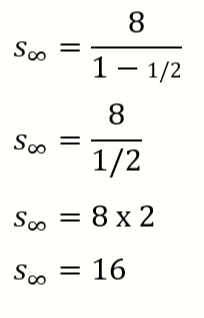
Jadi hasil jumlah S tak hingga nya adalah 16. Ingat ya, pada deret geometri tak hingga, kita dapat mencari jumlah dari keseluruhannya. Hal ini dikarenakan nilainya yang semakin mengecil dan mendekati 0.
Kira-kita seperti ini ya:
8 + 4 + 2 + 1 + 1⁄2 + 1⁄4 + … = 16
Nah, mudah kan?
Sekarang saatnya kita belajar tentang contoh soal deret geometri ya..
5# Contoh Soal Deret Geometri
1 . Hitunglah suku ke-10 dari barisan geometri berikut 1⁄8 , 1⁄4 , 1⁄2 , … !
Penyelesaian :
Diketahui :
- a =1⁄8
- r = 1⁄4 : 1⁄8
- r = 2
Ditanya :
- U10 = ?
Jawab :
- U10 = arn – 1
- U10 = 1⁄8 . 2 (10 – 1)
- U10 = 1⁄8 . 29
- U10 = 1⁄8 . 512
- U10 = 64
Jadi, U10 barisan geometri tersebut adalah = 64
2. Sebuah bakteri membelah diri menjadi 2 setiap 6 menit, berapakah jumlah bakteri setelah satu jam jika awalnya hanya terdapat 2 bakteri?.
Penyelesaian :
Diketahui :
- a = 2
- r = 2
- n = setelah 1 jam
- n = (1 jam/6 menit) + 1
- n = 60 menit / 6 menit + 1
- n = 10 +1
- n = 11
Ditanya :
- U11 = ?
Jawab :
Cara 1
- U11 = arn – 1
- U11 = 2. 2 (11 – 1)
- U11 = 2. 2 (10)
- U11 = 2. 1024
- U11 = 2048
Cara 2
Kita dapat membuat barisan geometri dari permasalahan tersebut. Jika disketsa, kira-kira sebagai berikut ini
Jadi, jumlah amoeba setelah 1 jam adalah 2048
3. Selembar kertas dipotong menjadi dua bagian. Setiap bagian dipotong menjadi dua dan seterusnya. Jumlah potongan kertas setelah potongan keenam sama dengan …
Penyelesaian :
Diketahui :
- a = 1
- r = 2
Ditanya :
- U5 = ?
Jawab :
- Un = arn – 1
- U6 = 2. 2 (6 – 1)
- U6 = 2. 2 (5)
- U6 = 2. 32
- U6 = 64
Jadi, potongan kertas setelah potongan keenam adalah 64.
4. Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. Suku ke-7 deret tersebut adalah ….
Penyelesaian :
Diketahui :
- a = 3
- U9 = 768
Ditanya :
- U7 = ?
Jawab :
Sebelum kita mencari nilai dari U7 , kita akan mencari nilai r terlebih dahulu.
Ingat kembali bahwa Un = arn – 1 sehingga U9 dapat ditulis menjadi
- U9 = ar(9 – 1)
- 768 = 3r(9 – 1)
- 768/3 = r(9 – 1)
- 256 = r(8)
- 8√256 = 8√r(8)
- 2 = r
- r = 2
Sehingga,
- U7 = ar(7 – 1)
- U7 = 3. 2(7 – 1)
- U7 = 3. 2(6)
- U7 = 3. 64
- U7 = 192
Jadi suku ke-7 deret tersebut adalah 192
5. Diketahui suku ke-5 dari barisan geometri adalah 243, hasil bagi suku ke-9 dengan suku ke-6 adalah 27. Suku ke-2 dari barisan tersebut adalah ….
Penyelesaian :
Diketahui :
- U5 = 243
- U9 / U6 = 27
Ditanya :
- U2 = ?
Jawab :
Sebelum kita mencari nilai dari U2 , kita akan mencari nilai a dan r terlebih dahulu.
Ingat kembali Un = arn – 1 maka
- U9 / U6 = 27
- ar(9 – 1) : ar(6 – 1) = 27
- ar(8) : ar(5) = 27
- r(8-5) = 27
- r(3) = 27
- r = 3√27
- r = 3
Selanjutnya, substitusikan r = 3 ke persamaan
- U5 = 243
- ar(5 – 1)= 243
- a. 3(4) = 243
- a. 81 = 243
- a = 243 / 81
- a = 3
Selanjutnya kita bisa mencari nilai U2
- Un = arn – 1
- U2 = 3. 3(2 – 1)
- U2 = 3. 3(1)
- U2 = 3. 3
- U2 = 9
Jadi, suku ke-2 dari barisan tersebut adalah 9
6. Jumlah 6 suku pertama deret geometri 2 + 6 + 18 + … adalah …
Penyelesaian :
Diketahui :
- a = 2
- r = U2 / U1
- r = 6/2
- r = 3
Ditanya :
- S6 = ?
Jawab :
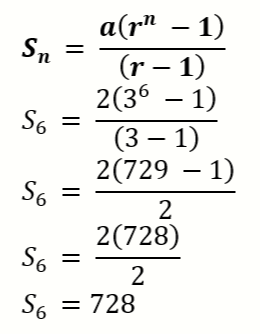
Jadi, jumlah 6 suku pertama deret geometri tersebut adalah 728.
7. Sebuah bola dijatuhkan dari ketinggian 5 m di lantai. Setiap kali memantul, bola mencapai ketinggian ½ kali tinggi sebelumnya, demikian seterusnya. Carilah jarak yang ditempuh bola tersebut sampai berhenti!
Jawab :
Cara 1:
Kalau memakai rumus biasa, maka caranya adalah :
(i) Jarak yang ditempuh pada waktu turun = 5+ 5/2+ 5/4
- a = 5/2 ; r = ½ ;
- S~ = a/1-r
- S~ = 5/1-½
- S~ = 5/½
- S~ = 10
(ii) Jarak yang ditempuh pada waktu naik = 5/2+5/4+5/8+…
- a = 5/2
- r = ½
- S~ = a/1-r
- S~ = (5/2) / 1-½
- S~ = 5
Jadi, jarak yang ditempuh bola tersebut = tinggi mula-mula + jarak tempuh turun + jarak tempuh naik
= (5 +10+10) m
= 15 m.
hmm… caranya cukup panjang ya?
Sekarang, kita coba pakai cara kedua. Cara ini biasa saya ajarkan pada Kursus CPNS secara tatap muka maupun pada Kursus CPNS Online.
Rumus cepat jarak tempuh bola sampai berhenti
= (b+a/b-a) × t
keterangan:
a = pembilang dari rasio
b = penyebut dari rasio
t = ketinggian bola
Sehingga
r = ½
a = 1
b = 2
t = 5m
maka:
- jarak tempuh bola = (b+a/b-a) × t
- = (2+1/2-1) × 5 meter
- = 3 × 5 m
- = 15 m
Jadi jarak tempuh bola sampai berhenti adalah 15 m.
Bagaimana? Lebih mudah dan lebih cepat pakai cara kedua kan?
6# Kuis Soal Barisan dan Deret Geometri
Nah, setelah mempelajari materi dan latihan soal tentang deret geometri, mari kita lihat sejauh mana penguasaan kamu melalui kuis yang bisa kamu kerjakan secara langsung.
Tapi sebelum memulai mengerjakan kuis, kamu perlu tahu dulu aturan mainnya:
- 1. Kuis berbatas waktu
- 2. Pilih jawaban dengan cara mengeklik salah satu opsi yang tersedia
- 3. Jika jawabanmu benar, maka opsi jawabanmu akan berwarna hijau
- 4. Jika jawabanmu salah, maka opsi jawaban terpilih akan berwarna merah
- 5. Untuk memulai mengerjakan kuis, klik tombol MULAI KUIS
Ini adalah kuis dengan batasan waktu. Anda akan diberikan waktu 600 detik untuk menjawab semua pertanyaan yang tersedia. Apakah Anda siap?
Diketahui barisan geometri dengan u1 = x3/4 dan u4 = x ∜ x. Rasio barisan geometri tesebut adalah …
Pertambahan penduduk suatu kota tiap tahun mengikuti aturan barisan geometri. Pada tahun 1996 pertambahannya sebanyak 6 orang, tahun 1998 sebanyak 54 orang. Pertambahan penduduk pada tahun 2001 adalah … orang.
tahun 1996 => u1 = a = 6
tahun 1998 => u1 = ar2 = 54
6.r2= 54
r2 = 9
r = 3
tahun 2001 => u6 = ar5
= 6.(3)5
= 1.458
Sebuah bola pingpong dijatuhkan dari ketinggian 25 m dan memantul kembali dengan ketinggian 4/5 kali tinggi semula. Pematulan ini berlangsung terus menerus hingga bola berhenti. Jumlah seluruh lintasan bola adalah … m.
Untuk mengerjakan soal ini kita bisa menggunakan rumus cepat :
jarak tempuh bola sampai berhenti = (b+a/b-a) × t
di mana:
a = pembilang (dari rasio) = 4
b = penyebut (dari rasio) = 5
t = tinggi bola = 25 meter
Sehingga,
(b+a/b-a) × t = ((5+4) / (5-4)) x t
= 9 x 25 m
= 225 m
Jadi, jumlah seluruh lintasan bola adalah 225 meter
Sebuah bola jatuh dari ketinggian 10 m dan memantul kembali dengan ketinggian 3/4 kali tinggi sebelumnya, begitu seterusnya hingga bola berhenti. Jumlah seluruh lintasan bola adalah …
Karena bola memantul terus-terusan sampai berhenti, berarti ini termasuk deret geometri tak hingga. Untuk mencari panjang lintasan bola yang memantul ini, rumus yang digunakan adalah
Panjang lintasan = ketinggian bola jatuh + 2(kali deret takhingga)
Dalam deret takhingga ini, yang menjadi suku pertamanya adalah pantulan pertama (bukan ketinggian bola jatuh pada awal).
Pantulan pertama = 10 x 3/4 = 30/4 m (suku pertama)
S∞ = a⁄1-r
= 30⁄4 : 1-3⁄4
= 30⁄4 : 1⁄4
= 30⁄4 x 4⁄1
= 30
Panjang lintasan = 10 + 2(30) = 70m
Jumlah deret geometri tak hingga adalah 7, sedangkan jumlah suku – suku yang bernomor genap adalah 3. Suku pertama deret tersebut adalah …
Deret geometri : a + ar + ar2 + ar3 + ar4 + ar5 + ar6 + …
Perhatikan suku genap dan ganjilnya, di mana pada suku-suku genap, suku pertamanya adalah ar dan pada suku-suku ganjil, suku pertamanya adalah a, dengan rasionya adalah r2.
Stakhingga = a / (1-r)
7 = a / (1-r)
7(1 – r) = a … (i)
Berdasarkan rumus jumlah deret geometri tak hingga diatas, maka kita memperoleh rumus deret geometri takhingga bersuku genap dengan mengganti suku awal dengan “ar” dan rasionya “r2“.
Sgenap = ar / (1-r2)
3 = ar / (1-r2)
3(1 – r2) = ar … (ii)
Substitusi (i) ke (ii), sehingga diperoleh :
3(1 – r2) = (7(1 – r))r
3 – 3r2 = 7r – 7r2
4r2 – 7r + 3 = 0
(4r-3)(r-1) = 0
r = 3/4 atau r = 1
substitusi nilai “r” tersebut ke persamaan (i), sehingga diperoleh :
untuk r = ¾
a = 7(1 – r) = 7(1 – 3/4) = 7/4
untuk r = 1
a = 7(1 – r) = 7(1 – 1) = 0

Seutas tali dipotong menjadi 7 bagian dan panjang masing–masing potongan membentuk barisan geometri. Jika panjang potongan tali terpendek sama dengan 6cm dan potongan tali terpanjang sama dengan 384cm, panjang keseluruhan tali tersebut adalah … cm.
u1 = a = 6
u7 = ar7-1 = 384
6.r6= 384
r6 = 64
r = 2
Sn= a(rn - 1) ⁄ r-1
S7 = 6(27 - 1) ⁄ 2-1
S7 = 6(128 - 1) ⁄ 2-1
S7 = 6 (127) / 1
S7 = 762
Di antara rumus barisan berikut ini, yang merupakan barisan geometri adalah ⋯ .
Barisan geometri memiliki rumus umum Un = arn−1. Perhatikan bahwa rumus barisan geometri hanya terdiri dari 1 suku (tidak ada penjumlahan dan pengurangan).
Opsi pertama: Un = 4n -5
Rumus barisan tersebut memiliki 2 suku (ada pengurangan) sehingga jelas bukan barisan geometri.
Opsi kedua: Un = 2n . n-2
Rumus barisan tersebut bukan termasuk barisan geometri karena variabel n muncul dengan posisi yang berbeda, yaitu sebagai pangkat dan basis.
Opsi ketiga: Un = 2n3 -1
Rumus barisan tersebut memiliki 2 suku (ada pengurangan) sehingga jelas bukan barisan geometri.
Opsi keempat: Un = n3 .2-n
Rumus barisan tersebut bukan termasuk barisan geometri karena variabel n muncul dengan posisi yang berbeda, yaitu sebagai pangkat dan basis.
Opsi kelima: Un = 2n+1.3-n
Perhatikan bahwa rumus barisan di atas dapat ditulis menjadi
Un = 2n.21 .1/3n
= 2. 2/3n
Bentuk rumus terakhir menunjukkan bahwa ini adalah barisan geometri dengan suku pertama
a= 2
dan rasio r=2/3
.
Sebuah mobil dibeli dengan haga Rp80.000.000,00. Setiap tahun nilai jualnya menjadi 3/4 dari harga sebelumnya. Berapa nilai jual setelah dipakai 3 tahun ?
Kata kunci dalam soal ini adalah “Setiap tahun nilai jualnya menjadi 3/4 dari harga sebelumnya”, ini artinya rasionya 3/4 dan termasuk dalam deret geometri.
Yang jadi pertanyaannya adalah suku ke-4 dengan a = 80.000.000
U4 = ar3
= 80.000.000(3/4)3
= 80.000.000(27/64)
= 33.750.000
7# Apalagi selanjutnya?
Akhirnya, kamu telah belajar tentang materi barisan dan deret geometri beserta latihan soal tentang deret geometri. Jika kamu merasa tulisan ini bermanfaat, silakan share kepada teman, saudara, atau tetanggamu dengan cara mengeklik salah satu icon media sosial di bawah tulisan ini. Atau kamu juga dapat mengcopy dan membagikan link tulisan ini melalui media sosial yang kamu miliki.
Dan jika kamu menghendaki latihan soal yang lebih lengkap untuk persiapan tes CPNS, kami sediakan kursus CPNS online yang bisa kamu ikuti melalui link berikut ini:
Kursus CPNS OnlineDemikian, semoga bermanfaat. Aamiin.
Sukses selalu untuk kita semua
Salam cerdas, LUAR BIASA.
Wiji Hatmoko
Wiji Hatmoko
Founder dan Owner Ciptacendekia.com ini menghabiskan sebagian besar waktunya untuk belajar sesuatu yang baru. Mulai dari blogging, SEO, design grafis, internet marketing, hingga metode belajar dan mengajar. Setelah sukses membuat Kursus Persiapan Tes Perangkat Desa dan Kursus CPNS yg berhasil meloloskan ratusan pesertanya kini ia juga sibuk membuat Kursus UTBK-SNBT untuk anak-anak SMA yang mau kuliah di Perguruan Tinggi Negeri. Ikutlah menyebarkan kebaikan dgn membagikan artikel di website ini atau memberikan feedback berupa komentar yg membangun. Selamat belajar!
Website : https://ciptacendekia.com
Arsip Posting
Link Latihan Soal CPNS
- Tes Wawasan Kebangsaan:
- a. Pancasila
- b. UUD 1945
- c. Bhinneka Tunggal Ika
- d. NKRI
- Tes Intelegensi Umum:
- a. Tes Kemampuan Verbal
- b. Tes Kemampuan Numerik
- 1) Tes Aritmetik
- 2) Tes Deret Angka
- 3) Tes Seri Huruf
- 4) Tes Logika Angka
- 5) Tes Angka dalam Cerita
- c. Tes Kemampuan Berpikir Logis dan Analisis
- 1. Tes Logika Umum
- 2. Tes Analisa Pernyataan
- 3. Tes Kesimpulan Silogisme
- 4. Tes Logika Cerita
- Tes Karakteristik Pribadi:
- a. Tes Integritas Diri
- b. Tes Semangat Berprestasi
- c. Tes Kreatifitas dan Inovasi
- d. Tes Orientasi pada Pelayanan
- e. Tes Kepekaan Terhadap Orang Lain
- f. Tes Kemampuan Beradaptasi
- g. Tes Kemampuan Mengendalikan Diri
- h. Tes Kemampuan Bekerja Mandiri dan Tuntas
- i. Tes Kemauan dan Kemampuan Belajar Bekelanjutan
- j. Tes Kemampuan Bekerja Sama dalam Kelompok
- k. Tes Kemampuan Menggerakkan dan Mengkoordinir Orang lain
![KURSUS CPNS ONLINE [TERLENGKAP DI INDONESIA] Kursus CPNS Online Soal 2024 Tipe HOTS](https://ciptacendekia.com/wp-content/uploads/2022/11/Kursus-CPNS-Online-Soal-Tipe-HOTS.webp)

0 Tanggapan pada "Deret Geometri, Rumus Deret Geometri, sampai Latihan Soal Deret Geometri"